

#Limits calculus examples how to
Left hand derivative and right hand derivativeġ3. The following are 30 code examples for showing how to use scipy. In fact, early mathematicians used a limiting process to obtain better and better approximations of areas of circles. Some properties of continuous functionsġ1. The concept of a limit or limiting process, essential to the understanding of calculus, has been around for thousands of years. Here is one de nition: lim(1 + x)1 x x0+ way to evaluate this limit is make a table of numbers. If a function is continuous at all the point in an interval, then it is said to be a continuous in that interval.ĩ. lim(1 + x)1 x x0+ way to evaluate this limit is make a table of numbers. If there is any break at the point x = a then we say that the function is not continuous at the point x = a. A function f( x) is continues at x = a if its graph has no break at x = a Methods of evaluation of algebraic limitsīefore going into the topic, let us first discuss about the continuity of a function. Indeterminate forms and evaluation of limitsĦ. List of Limit Laws Constant Law limxakk Identity Law limxaxa Addition Law limxaf(x)+g(x)limxaf(x)+limxag(x) Subtraction Law limxaf(x)g(x). Algorithm of right hand limit : R x = aĥ.

Limits are used when we have to find the value of a function near to some value.Ģ. (Remember, infinity is not a real number.In this section, we will discuss about limits, continuity of a function, differentiability and differentiation from first principle. Continuity Continuity of a graph is loosely defined as the ability to draw a graph without having to lift your pencil. Substituting 0 for x yields 5/0, which is meaningless hence, DNE. This tutorial with examples covers the concept of limits, differentiating by first principles. Substituting 0 for x yields 0/5 = 0 hence, Calculus is a branch of mathematics that studies rates of change. Velocity is computed by a limit (it the derivative of the position), as well as acceleration (which is the derivative of.

Simplifying the compound fraction, you find that to use limits in your everyday life, try walking half of the way to school, then half of the distance remaining after that, then half of the way you still have to go, then. Substituting 3 for x yields 0/0, which is meaningless. The graph of (x 2 − 9)/(x + 3) would be the same as the graph of the linear function y = x − 3 with the single point (−3,−6) removed from the graph (see Figure 1).įigure 1 The graph of y = ( x 2 − 9)/( x + 3). Factoring first and simplifying, you find that Substituting −3 for x yields 0/0, which is meaningless. When x is replaced by 2, 3 x approaches 6, and 3 x − 1 approaches 5 hence. Some of these techniques are illustrated in the following examples.Įxample 1: Find the limit of the sequence:īecause the value of each fraction gets slightly larger for each term, while the numerator is always one less than the denominator, the fraction values will get closer and closer to 1 hence, the limit of the sequence is 1. Limits of functions are evaluated using many different techniques such as recognizing a pattern, simple substitution, or using algebraic simplifications. Example: the limit of start fraction 1 divided by x minus 1 end fraction as x approaches 1. to use the Integral Calculator, go to Help or take a look at the examples.
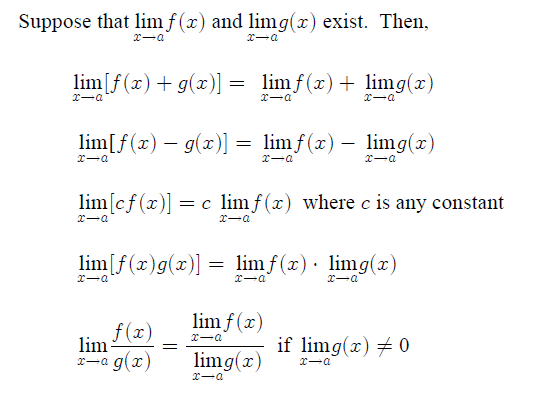
Differentiation of Exponential and Logarithmic Functions.Differentiation of Inverse Trigonometric Functions It is important to analyze and become acquainted with the concept of limits because many of the concepts in the study of calculus and other scientific branches of study use the limit of a. This document details how each of the sample free-response questions in the course and exam description (CED) would be scored.Limits Involving Trigonometric Functions.


 0 kommentar(er)
0 kommentar(er)
